Square lattice
A square lattice.
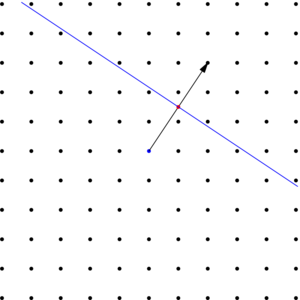
Connect origin to random point and take the perpendicular bisector. This is a bragg plane (line).
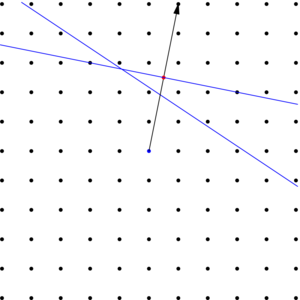
Repeat for most points nearby.
This is what it looks like after a while.

Connect the origin to a random region. Each time you cross a line (bragg plane), you are in a new (+1) brillouin zone.
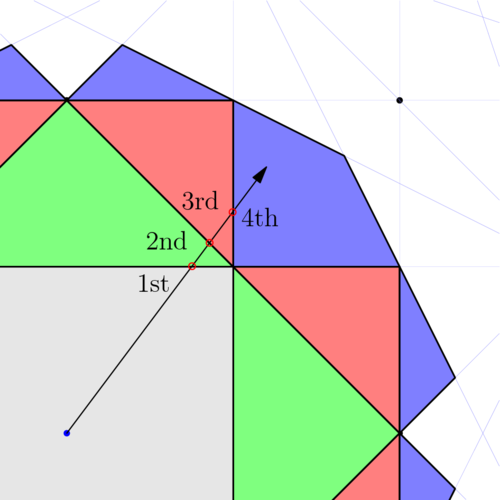
These are the first four brillouin zones for the square lattice.
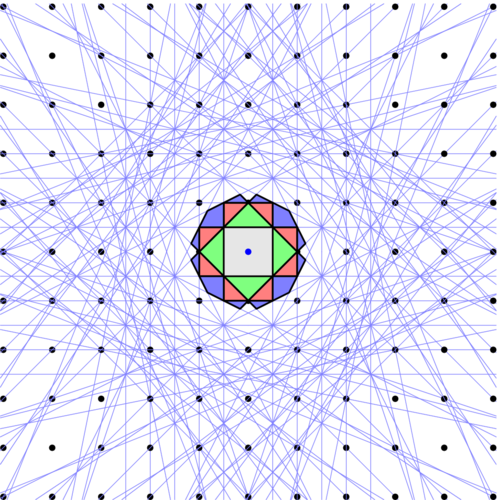
First four brillouin zones, zoomed.
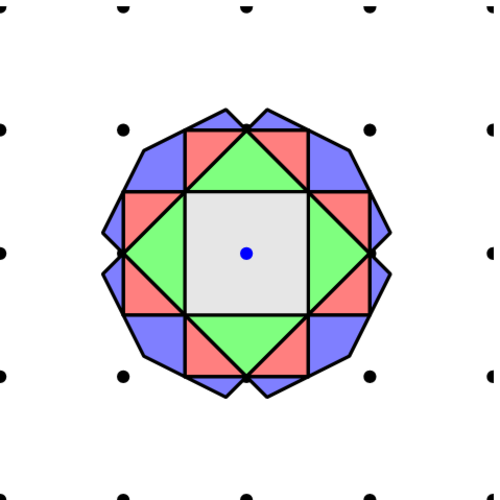
Hexagonal lattice
A hexagonal lattice.

Bragg planes of the hexagonal lattice.

First four brillouin zones.
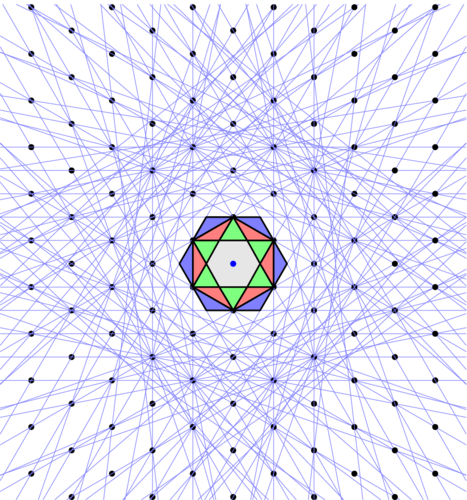
First four brillouin zones, zoomed.
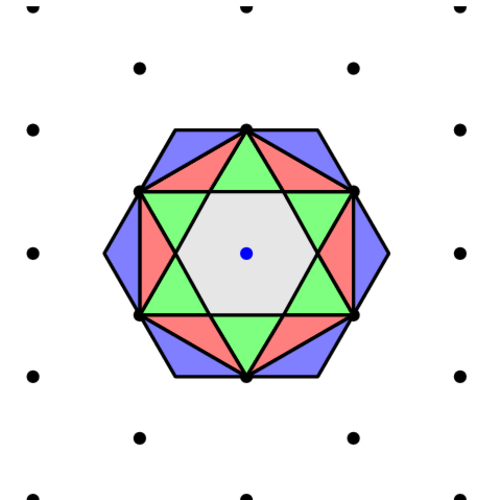
Code for diagrams
Diagrams made in asymptote:
size(8cm,0);
unitsize(1cm,1cm);
import geometry;
pair O=(0,0);
pair a, mid;
line l,lp;
dot(O,blue);
int N = 5;
fill((-N,-N)--(-N,N)--(N,N)--(N,-N)--cycle,white);
// Lattice and bragg planes.
for (int i=-N; i<=N; ++i) {
for (int j=-N; j<=N; ++j) {
a = (i,j);
if (a == O) continue;
dot(a);
l = line(O,a);
mid=(O+a)/2.;
lp = perpendicular(mid,l);
draw(lp,lightblue+0.3);
}
}
// 1st brillouin zone for square lattice.
filldraw((0.5,0.5)--(-0.5,0.5)--(-0.5,-0.5)--(0.5,-0.5)--cycle, lightgrey);
// 2nd brillouin zone for square lattice.
filldraw((0.5,0.5)--(1,0)--(0.5,-0.5)--cycle,lightgreen,black+0.2);
filldraw((0.5,-0.5)--(0,-1)--(-0.5,-0.5)--cycle,lightgreen,black+0.2);
filldraw((-0.5,-0.5)--(-1,0)--(-0.5,0.5)--cycle,lightgreen,black+0.2);
filldraw((-0.5,0.5)--(0,1)--(0.5,0.5)--cycle,lightgreen,black+0.2);
dot(O,blue);
// Example plane.
a = (1,5);
draw(O--a,Arrow);
l = line(O,a);
mid=(O+a)/2.;
dot(mid,red);
lp = perpendicular(mid,l);
draw(lp,blue);