[ Get the code at github ]
We’re using RK4 to solve:
$$ \begin{aligned} \frac{df_1(x)}{dx} = & 1 - f_2(x)\\ \frac{df_2(x)}{dx} = & f_1(x) - x \end{aligned} $$
with initial conditions:
$$\begin{aligned} x_0 &= 0\ f_1(x_0) &= 1\ f_2(x_0) &= 0 \end{aligned}$$
in the range $$[0,3]$$.
See the introductory post for details.
As already noted, the code below will be rather idiomatic for each language.
J
[ J is a terse array programming language. It’s on GPLv3 since March 2011 ]
Resisting the temptation to reduce the code to a line of illegible, swear-like bunch of characters, here is the full code in just 8 crystal clear lines.
NB. Assuming given:
NB. Fs: Functions (as gerund)
NB. dx: dx step
NB. v: initial values list
step =: 3 : 0
a =: (Fs`:0) ({:v)
b =: (Fs`:0) ({:v) + 2%~dx*(1,a)
c =: (Fs`:0) ({:v) + 2%~dx*(1,b)
d =: (Fs`:0) ({:v) + dx*(1,c)
D =: dx*6%~+/(1 2 2 1) * |:(a,.b,.c,.d)
v =: v, (({:v) + (dx, D))
)
Extendable, expandable, short.
For example:
F1 =: 3 :'1 - 2{y'
F2 =: 3 :'-/ 1 0 { y'
Fs =: F1`F2
dx =: 0.01
v =: ,:0 1 0 NB. Vector of initial values 'x0, y1, y2'
(step^:300) 0 NB. Run 300 steps
That gives us the vector v with all the value-pairs $$(x,y1,y2)$$
v
0 1 0
0.01 1.00995 0.00999983
0.02 1.0198 0.0199987
0.03 1.02955 0.0299955
0.04 1.0392 0.0399893
0.05 1.04875 0.0499792
...
2.97 1.98469 0.170752
2.98 1.99303 0.16089
2.99 2.00147 0.151013
3 2.01001 0.14112
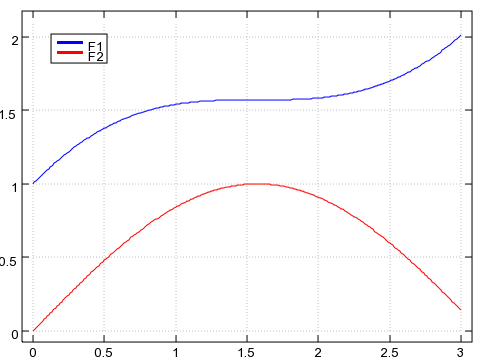
which we can conveniently plot:
load 'plot'
'key f1, f2' plot ({. ; (1 { ]) ,: 2 { ]) |: v
LISP
(defun next-y-rk4 (x y F h)
(let ((k (list y)))
(dolist (m '(0 .5d0 .5d0 1))
(push (mapcar #'(lambda (x) (* h x))
(mapcar #'apply F (loop repeat (length F) collect
(mapcar #'(lambda (a b) (+ a (* m b))) (cons x y) (cons h (first k))))))
k))
(mapcar #'(lambda (x k1 k2 k3 k4) (+ x (/ (+ k1 (* 2 k2) (* 2 k3) k4) 6)))
y (fourth k) (third k) (second k) (first k))))
(defmacro solve-rk4 (initial-values x0 x1 h F)
`(let ((y ,initial-values) (result nil))
(loop for x from ,x0 below ,x1 by ,h do
(setf y (next-y-rk4 x y ,F ,h))
(push (cons (+ ,h x) y) result))
(reverse result)))
For example:
(defun f1 (x y1 y2)
(- 1 y2))
(defun f2 (x y1 y2)
(- y1 x))
(defparameter *h* 0.01d0 "Step for RK4")
(defparameter *initial-values* '(1.0d0 0.0d0) "Initial values f1(x0), f2(x0), ...")
(defparameter *x0* 0.0d0)
(defparameter *x1* 3.0d0)
(setf v (solve-rk4 *initial-values* *x0* *x1* *h* '(f1 f2)))
which is indeed the same solution as before:
(loop for i from 0 below 5 do (format t "~{~,5f ~}~%" (nth i v)))
0.01000 1.00995 0.01000
0.02000 1.01980 0.02000
0.03000 1.02955 0.03000
0.04000 1.03920 0.03999
0.05000 1.04875 0.04998
(loop for i from 5 downto 1 do (format t "~{~,5f ~}~%" (nth i (reverse v))))
2.96000 1.97644 0.18060
2.97000 1.98469 0.17075
2.98000 1.99303 0.16089
2.99000 2.00147 0.15101
3.00000 2.01001 0.14112
Coming up: R, Fortran, Python, Haskell, Pari/GP, maxima.
Any other languages that you would like to see?