Triangle's inner point.

2010 Jul 08

[ See the C code at bitbucket ] [ See the diagram’s code at bitbucket ]

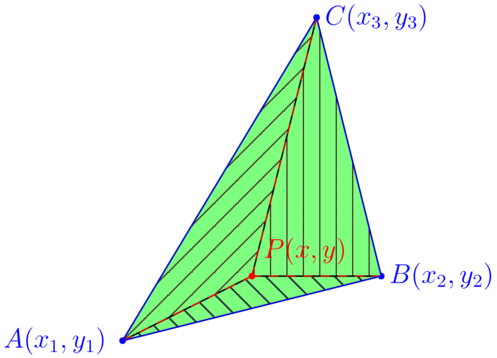
Suppose you have a point $$P(x,y)$$ and a triangle $$ABC$$ defined by it’s vertices: $$A(x_1,y_1), B(x_2, y_2), C(x_3, y_3)$$. How can you tell if $$P$$ is inside $$ABC$$?

One simple way to test that, is to compare triangle’s areas: the area of the triangle $$ABC$$ is equal to the sum of the smaller triangles formed by $$P$$ only if $$P$$ is an inner point. That is:

triangle_pin triangle_pout

Inner point:

$$\textrm{E}(ABP) + \textrm{E}(CBP) + \textrm{E}(ACP) = \textrm{E}(ABC)$$

Not an inner point:

$$\textrm{E}(ABP) + \textrm{E}(CBP) + \textrm{E}(ACP) \neq \textrm{E}(ABC)$$

where the area of a triangle is simply:

$$\frac{1}{2}|x_1y_2 + x_2y_3 + x_3y_1 - y_1x_2 - y_2x_3 - y_3x_1|$$

Testing with C and allegro

I used the code below for a quick “test” of the method. In this code, we first generate a random triangle. Then, we test if the mouse pointer (representing point P), is inside or outside that triangle. If it’s in, we paint the triangle yellow(ish), if not, we paint it blue.

#include <stdio.h>
#include <allegro.h>
#include <stdlib.h>
#include <time.h>


#define SWIDTH 640
#define SHEIGHT 480

BITMAP *buffer = NULL;

struct point {
    int x;
    int y;
};

struct triangle {
    struct point A, B, C;
};


double E(struct point A, struct point B, struct point C)
{
    int x1 = A.x, x2 = B.x, x3 = C.x;
    int y1 = A.y, y2 = B.y, y3 = C.y;
    return .5*abs(x1*y2 + x2*y3 + x3*y1 - y1*x2 - y2*x3 - y3*x1);
}

int inner(struct triangle T, struct point P)
{
    if (E(T.A, T.B, P) + E(T.A, T.C, P) + E(T.B, T.C, P)  ==
            E(T.A, T.B, T.C))
        return 1;
    return 0;
}

void world(struct triangle T, int color)
{
    int x1 = T.A.x, x2 = T.B.x, x3 = T.C.x;
    int y1 = T.A.y, y2 = T.B.y, y3 = T.C.y;
    clear_bitmap(buffer);

    triangle(buffer, x1, y1, x2, y2, x3, y3, color);

    blit(buffer,screen, 0, 0, 0, 0, SCREEN_W, SCREEN_H);
}

int main(void)
{
    int pos;
    struct point P;
    struct triangle T;

    allegro_init();
    install_keyboard();
    install_mouse();
    show_os_cursor(MOUSE_CURSOR_ARROW);
    set_gfx_mode(GFX_AUTODETECT_WINDOWED, SWIDTH, SHEIGHT, 0, 0);

    buffer = create_bitmap(SWIDTH, SHEIGHT);

    srandom(time(0));
    T.A.x = random()%SWIDTH; T.A.y = random()%SHEIGHT;
    T.B.x = random()%SWIDTH; T.B.y = random()%SHEIGHT;
    T.C.x = random()%SWIDTH; T.C.y = random()%SHEIGHT;

    while(!key[KEY_ESC]) {
        rest(150);
        pos = mouse_pos;
        P.x = pos >> 16;
        P.y = pos & 0x0000ffff;
        if (inner(T,P))
            world(T, makecol(200,200,50));
        else
            world(T, makecol(50,50,200));
    }

    return 0;
}
END_OF_MAIN()